Zur
Datenschutzerklärung
zu den schweinelogischen Grundlagen
Der Beweis schweinischer
Sätze
ausbaufähige
Diplomarbeit zu vergeben!
Schweinische
Aussagen unterscheidet man in 2 Sorten:
1)
Existenzaussagen vom Typ"Es gibt..."
Beispiel:
"Es gibt Bauern, die kannst du vergessen."
So etwas beweist
ein Schwein, indem es Dir genüßlich so lange etwas vorschmatzt
-grunzt und -suhlt, bis Du völlig vergessen hast, dass der
stolze Bauer hinter Dir Dir auch noch seine Frau vorstellen
wollte, die im Nachbarkoben gerade den Eber ...
...aber das
führt jetzt vom Thema ab. Jedenfalls wird diese Existenzaussage
durch EIN Beispiel bereits bewiesen.
2)All-Aussagen
vom Typ "Für alle ... gilt ...: ..." oder "Wenn
..., dann ..."
Beispiel:
"Für alle viereckigen Koben gilt: Die Summe der Innenwinkel
beträgt 360 Grad."
Weil es
unendlich viele viereckige Koben gibt, ist es unmöglich, diesen
Satz zu beweisen, indem schwein noch so viele viereckige Koben
vorzeigt. Es könnte ja immer noch viereckige Koben geben, deren
Innenwinkel-Summe von 360 Grad abweicht.
Schweine
haben aber einen geschärften Sinn für das Wesentliche und
Einfache und somit unter Berücksichtigung ihrer
aussergewöhnlichen kognitiven Fähigkeiten Methoden entwickelt,
die einem die Richtigkeit solcher Aussagetypen klar machen. Diese
Methoden heissen
Beweise. Es gibt 4 wichtige Arten
davon:
Beweis
durch Nachschnüffeln
|
Widerborstigkeits-Beweis
|
Säumetrie-
Beweis
|
Konnigrunzt-
Beweis.
|
Bei jedem Beweis
unterscheidet man 3 Teile:
1)Genaue Formulierung aller Voraussetzungen
(Vor.)
2)Genaue Formulierung der Behauptung
(Beh.)
3)Begründung der
Behauptung unter Verwendung der Voraussetzungen und
schon bekannter Sätze und Definitionen (Bew.)
Beweis
durch Nachschnüffeln:
| 1) Ein etwas bruthales Beispiel: Ein
Eber ist an einem Wandring einer Scheune mit einem Seil
festgebunden. Es ist meist straff gespannt, da er seinen
Bewegungsradius wg. Freiheitsdrang natürlich voll
auslotet. Nun merkt er aber trotzdem, etwas seltsames:
Seine extremen Schubberstellen an der Holzwand erscheinen
genau dann immer unter einem Blickwinkel von 90 Grad,
wenn er extrem am Seil zieht. Wenn nicht, muss er seinen
Kopf weiter drehen, um von der einen Schubberstelle zu
der anderen zu schauen. Er schüttelt den Kopf und denkt
sich:
w(MAE) =
d*, da
das Dreick MAE gleichschenklig sein muss,
w(MBE)=e*, da das Dreieck MBE
gleichschenklig sein muss.
(d*+e*) +
e* + d* = 2d* + 2e* = 2(d* + e*) =180°(Satz von der Winkelsumme im
Dreieck)
=>
d* +e* = 90° !!!
|
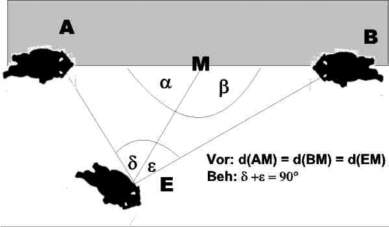
Abweichung vom Text:
"w(MEA)" = d* heißt
"Winkel an E im Dreieck MEA"
"w(MEB)" = e* heißt "Winkel an E im
Dreieck MEB" |
| 2)
Bei der gefälligen Betrachtung
seines wuseligen Harems rechnet der Eber auch: Eine
dreistellige Ferkelzahl ist zu gleichen teilen 9 Säuen
als Tankstellen zuzuordnen, wenn ihre Quersumme durch 9
teilbar ist. Vor.:
a sei die
Hunderterziffer, b die Zehnerziffer und c die
Einerziffer.
Beh.:100a + 10 b + c ist durch 9
teilbar.
|
Bew.: 100a +10b+c = (a + b + c )
+99a + 9b a + b + c ist die Quersumme und nach Vor.
durch 9 teilbar. Ebenso sind 99a und 9 b unabhängig von
a und b jeweils durch 9 teilbar.
Wenn jeder Summand durch 9 teilbar ist , kann 9
überall ausgeklammert werden, und die Gesamtsumme ist
auch durch 9 teilbar.
|
Widerborstigkeitsbeweis:
Zu beweisen ist die
Behauptung: A => B.
Statt dessen beweist man
widerborstig die gleichwertige Kontraposition: nicht B => nicht A
siehe Schweinische
Logik
| Beispiel1) Ein Schwein steht mitten im Mittelweg des
Schweinestalls. Es passt genau zwischen die Kobenwände.
Da es sich gern zwei Fluchtwege offenhalten will, hofft
es: "Lass sie parallel sein!" Statt jetzt den
Hintern zusammenzu kneifen und lange zu überlegen, ob
die Wände parallel sind, weil sie ein gemeinsames Lot
haben (Bild1), stellt es die kontra-po-sitorische
Überlegung im Kopf an: Wenn die Wände sich treffen
würden, hätten sie kein gemeinsames Lot.(Was ein Lot
ist, weiss im Gegensatz zur Schülern JEDE Sau.) Vor.:
l ist senkrecht zu g, und l ist auch senkrecht zu h (A)
Beh.: G || h. (B)
Bew.: Annahme: g und h treffen sich in S (nicht B)
=> Die Winkel im Dreieck ABS haben die Summe 180°.
Da der Winkel bei S größer als 0 sein muss, müssen
die beiden übrigen Winkel zusammen kleiner als 180°
sein => Es ist also unmöglich, dass beide
gleichzeitig 90° aufweisen können.
Was dem Schwein einleuchtet ...
|
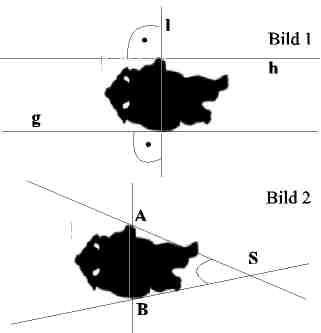 |
Säumetriebeweis:
| Schweine lieben als intelligente Tiere einfache
Formen. Besonders Eber - bei Säuen. Auf diese Art und
Weise müssen sie sich nicht allzu viel Gedanken machen ,
von welcher Seite sie sich ihnen nähern und wie sie ohne
unnötige Verrenkungen Anschluß finden können. Deswegen
sind die begehrtesten Säue in vielerlei Hinsicht
säumetrisch
gebaut(siehe Bild! und hier). Man
spricht von Achsensäumetrie(AS), wenn eine säumetrische
Achse zu erkennen ist, und bei 2 Achsen von
Punktsäumetrie( PS). Aus diesen Begriffen leiten sie
logischer Weise auch einfache Gesetze ab. |
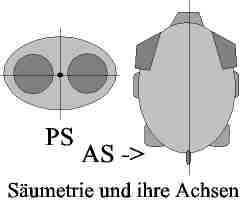
|
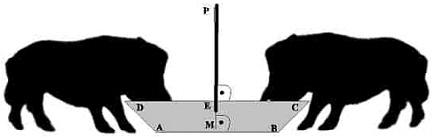
Beispiel:
2 Eber müssen getrennt
gehalten werden. Als Schweine legen sie auch bei den
Stalluntensilien Wert auf Säumetrie. Da verwundert es
nicht, dass ihr Schweinetrog ein Prisma ist. dessen
Querschnittsfläche ein säumetrisches Trapez ist. Da mit
dem Säumetriewunsch auch ein erhöhtes
Gerechtigkeitsempfinden gekoppelt ist, erklärt ihnen der
Bauer, dass er den Trog in die Zwischenwand der beiden
Koben integriert - und zwar mit einer abgehängten Wand
GENAU über der Längsachse des mit der Wasserwaage
ausgerichteten Troges. Das würde für beide eine gleiche
Futter"fläche" bedeuten. Auf Grund eines
säumetrischen Beweises akzeptieren sie.
|
Vor.: 1)Das Trapez ABCD ist
symmetrisch.
2)M ist Mittelpunkt von der Strecke AB.
3)Die Strecke PM ist infolge der
Schwerkraft genau senkrecht zu der Strecke AB.
Beh.: d(DE) = d( EC)
Aus 2.) und 3.) folgt, dass die Gerade
g(PM) säumetrische Achse zum Trapez ist. Damit liegen
auch C und D säumetrisch zu g(PM). Da die Achse die
Verbindungslinie zweier säumetrischer Punkte halbiert,
ist d(DE) = d (EC).
Was die Eber einsehen...
|
| Der schweinische Kusssatz: Da
Schweine keine Hemmungen haben, sich ausgiebig aufs Maul
zu schauen, haben sie mittels säumetrischer
Verschiebungen ein eigenes Rechengesetz gefunden. Ein
Kuss mit geöffneter Schnauze führt damit nicht zum
direkten Sex, sondern dazu, Acht aufeinander zu haben!
Bei den Hauern der Eber scheint das allerdings sehr
sinnvoll - besonders, wenn sie schwul sind.
|

|
Konnigrunztbeweis:
Diese Methode
führt auf Konnigrunzt - Sätze zurück.
Konni war eine
sehr schlaue Sau aus der Zeit, als die Pizzen noch dreieckig
waren.Sie liebte dies Dinger heiss und innig und ließ sich sogar
damit dressieren. Jedesmal, wenn sie Übereinstimmungen
feststellte, grunzte sie laut und vernehmlich. Dadurch bekam sie
einen Arbeitsplatz in der Endkontrolle bei einem renommierten
Pizzafabrikanten, und wenn nicht der Pizza -TÜV (*)und der Trend
zu LEAN- Production dazwischen gekommen wären, wäre sie da noch
heute und nicht in der Wurst.Sie hatte ein scharfes Auge und
reagierte dabei auf folgende Beobachtungen - d.h.
Übereinstimmungen, die sonst kein Schwein erkannt hätte:
| SSS: in allen drei Seiten
|
SWS: in zwei Seiten und dem Zwischenwinkel
|
WSW: in einer Seite und den beiden anliegenden
Winkeln
|
SWW: in einer Seite, einem anliegenden und einem
nicht anliegenden Winkel
|
SsW: in 2 Seiten und dem Gegenwinkel der größeren
Seite
|
(*) Die Leute
rammten sich bei excessivem Genuss immer öfter die Pizzaecken in
die Augen und erhoben Schmerzensgeld- unf sonstige
Regreßforderungen. Das führte dazu, dass die Pizzen unter
Inkaufnahme von Leerstellen auf dem Backblech abgerundet werden
mussten.
| Wie gesagt, Schweine haben einen geschärften
Blick für das Einfache und Wesentliche.
Eine
wesentlicher Gegenstand der Aufmerksamkeit ist dabei die
Strumpfbandlinie,
die in der Mitte des ABS- Systems senkrecht
zur Schenkelachse verläuft. Auch Eisbeinfreunde
schätzen diesen Region als Leckerbissen. (ABS =
Ausserordentlich beeindruckende Sau )
Aus einer darüber hinaus trotzdem noch etwas
verklärten Sichtweise folgt das nächste Beispiel:
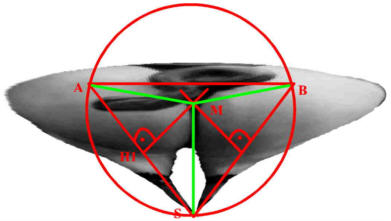
Im gleichschenkligen Dreieck einer säumetrischen
Schönheit treffen sich die Mittelsenkrechten der
"gleichen" Schenkel immer in dem Punkt, um den
sich für den Eber alles dreht.
|
Vor.:
Das Dreieck ABS ist
gleichschenklig.(V1). H1 und H2 halbieren die Schenkel.
(V2).Die Strecken HM sind jeweils senkrecht zu den
zugehörigen Schenkeln.(V3) Beh.: Die
Strecken AM, BM und SM sind gleich lang: d(AM) = d(BM)
=d(SM)
Bew.:
Das Dreieck ABS ist gleichschenklig und somit
achsensäumetrisch bezüglich der Geraden durch S und M.
Aus der Säumetrie V1 folgt : (H1 M) = d(H2 M)
Aus V2 folgt: d(A H1) = d(H1 S) und d(B H2) = d(H2 S)
Aus V3 folgt die Existenz der beiden eingezeichneten
rechten Winkel.
Nach dem Konnigrunzt-Satz SWS folgt:
Die Dreiecke (A H1 M) ,(B H2 M) , (S H1 M) und (S H2
M) sind kongruent.
Und daraus folgt:
Die Strecken (AM), (BM) und (SM) sind gleich lang.
|
Wird suhlend
fortgesetzt und überschnüffelt!





