Zur
Datenschutzerklärung
MATHE - Aufgabenberater
zurück
Standardaufgaben in der
Sek II -Analysis
Kurvendiskussion -
Steckbriefaufgaben:
Übersetzungshilfen
Beispiel:Sei P(a|b) der jeweils
gegebene Punkt und f(x) = tx ³+ux²+vx+w (--> f´(x) =
3tx²+2ux+v --> f´´(x) =6tx+2u )
| Text in der Aufgabe |
Umsetzung |
Einsetzung am Beispiel |
| f geht durch P f schneidet die x- Achse an den
Stellen d und e
f hat an P einen Extremum (Hoch- oder Tiefpunkt)
f berührt die x-Achse an der Stelle g
f Hat an P einen Wendepunkt
f hat an P die Steigung m
Die Wendetangente in P hat die Steigung m
f berührt die Gerade mit y = mx +n in P
f ist symmetrisch zur Y-Achse
f ist symmetrisch zum Ursprung
P ist Sattelpunkt
|
f(a) = b f(d) = 0 und f(e) = 0
f´(a) = 0
f(g) = 0 und f`´(g) = 0
f´´ (a) = 0
f´(a) = m
f´´(a) = 0 und f´(a) = m
f´(a) = m
alle Funktionsglieder mit ungeraden Potenzen entfallen
alle Funktionsglieder mit geraden Potenzen entfallen
f´(a) ==0 und f´´(a) =0
|
b = ta³+ua²+va+w 0 = td³+ud²+vd+w und 0 =
te³+ue²+ve+w
0 = 3ta²+2ua+v
0 = tg³+ug²+vg+w und 0 = 3tg²+2ug+v
0 =6ta+2u
m = 3ta²+2ua+v
0 = 6ta+2u und m = 3ta²+2ua+v
m = 3ta²+2ua+v
f(x) = ux²+w --> f´(x) = 2ux --> f´´(x) = 2u
f(x) = tx³+vx --> f´(x) = 3tx²+ v -->
f´´(x) = 6tx
0 = 3ta²+2ua+v und 0 =6ta+2u
|
Weitere Aufgaben:
|
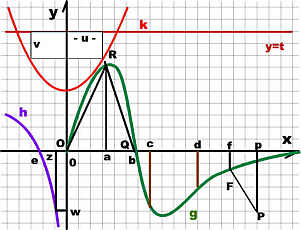
Gesucht bezüglich der Funktion g(grün): 1)
Der minimale Abstand |PF|:
P gegeben, F c g.
2)Das Dreieck ORQ mit maximalem Flächeninhalt
3)Der Flächeninhalt zwischen X-Achse und g
für [b,oo[
4)Die Lage eines 3 Längeneinheiten breiten
Streifens in der Fläche ausAufgabe3,der größten
Flächeninhalt hat.
|
Gesucht bezüglich der Funktion h(blau): 5)
Die von h und den Koordinatenachsen eingeschlossene
Fläche.
Gesucht bezüglich der Funktion k (rot):
6) Der maximale Flächeninhalt des
einbeschriebenen Rechtecks.
|
Hinweise dazu:
Int(b;p) bedeutet "Integral in den Grenzen
von b bis p"
| 1)Sei P =(p|y) |PF| =sqrt[(p-f)²+(y-g(f))²]
(Pythagoras in rechtwinkligem Hilfsdreieck)
|PF|ist minimal <=>(|PF|)´=0
--> f -->F -->|PF|
|
2) F = (1/2)*b*g(a) für 0<r<b F maximal
<=> F´= 0
--> r max
--> F max
|
3)lim (p--> oo)Int(b;p)[g(x)dx] |
| 4)|Int(c;c+3)[g(x)dx]| =F°(b) (b<c<oo)
F° max <=> F°´=0
--> c max --> F°max
|
5)F =z*w +|Int(e,z)[h(x)dx]| lim(w-->-oo)F =
lim(z-->0) F(z)
|
6)R=2*u*v)=2*u*(t-k(u)) R max >=> R ´ = 0
-->u --> R
max
|
Funktionenscharen
Jeder Buchstabe ausser x , der
bei einer Kurvendiskussion in einer Funktionsgleichung
(z.B.f[(x(t)]) auftaucht, ist als Konstante zu werten und wird
als solche in die ganz normale Berechnung einzufügen. Sie taucht
dann meist auch in den Ergebnissen wieder auf. Diese müssen dann
noch einmal diskutiert werden, weil dabei Wurzeln, Parabeln,
Brüche u.a. auftreten können.
Standardproblem A:
Zeigen Sie, dass sich alle Funktionen der Schar in zwei
Punkten schneiden!
Dabei betrachtet man in
f[x(t´)] =f[(x(t´´)] . Die Gleichung löst man dann nach x auf
und erhält die x- Koordinate der eventuellen Schnittpunkte.
Beispiel: f(x)=tx²+1 ----->
t´x² -t= t´´x²-t´´ ---> x²(t`-t´´)=´-t´´ +t´
--> x²= (t´-t´´ )/( t´-t´´) --> x²=1 --> x1 = 1
; x2 = -1
Standardproblem B:
Zeigen Sie, dass alle Wendepunkte( Extrema) auf dem Graphen der
Funktion g liegen! (Ortslinie)
Die errechnete Lösung für edie
Wendepunkte sei z.B. W(2t | 3/t). Das heißt: x = 2t und y = 3/t.
Verfahren: Man berechnet aus der
ersten Beziehung t und setzt den erhaltenen Wert in die zweite
ein: t=x/2 ---> y= 3/(x/2) ---> y= 6/x
y = 6/x ist die gesuchte
Funktionsgleichung für g.
