Zur
Datenschutzerklärung
MATHE - Aufgabenberater
zurück
Lösung eines 3x3
(incl.2x2) -Systems von linearen Gleichungen
Eine lin.Gl. mit drei
Variablen beschreibt in der reellen Welt eine Ebene(z.B.
Zimmerwand oder -Decke, allerdings auch die Wände und die Decke
einer vom Sturm gebeutelten windschiefen Holzscheune .) Hier wird
der Schnittpunkt von drei Ebenen bestimmt - etwa die Zimmerecke
oben rechts. Sollten 2 oder mehrere Ebenen aber parallel sein,
(z.B. Boden, Decke und eine Wand)was so auf den ersten Blick
nicht zu ersehen sein muss, dann gibt es diese Ecke nicht.
Sollten alle drei Ebenen parallel sein - etwa Böden in einem
mehrstöckigen Haus) ist ebenfalls Feierabend.Ebenso können zwei
oder drei Ebenen identisch sein - dann gibt es als Sonderlösung
eine Gerade oder die gesamte Ebene.
1.Schritt:
Suche aus A,B,C ein Gleichungspaar
heraus. Multipliziere die Gleichungen jeweils so mit Faktoren,
dass bei einer Addition eine Variable herausfällt.
2.Schritt: Suche ein anderes
Gleichungspaar heraus und lass bei demselben Verfahren dieselbe
Variable herausfallen.
3.Schritt: Du erhältst somit ein
2x2 System der Gelichungen D und E, das du ebenso wie in Schritt
1 abarbeitest.Dabei können prinzipiell drei Ergenisse für F
auftreten:
I) 0 = 0 -dann hat das
System unendlich viele (Sonder-)Lösungen. II) 0 /= 5, dann hat
das System keine Lösung. III) y (oder x oder z) = eine Zahl -->
4.Schritt: Diese wird dann in eine
Gleichung des 2x2-Systems eingesetzt, um die nächste Variable
auszurechnen.
5.Schritt: Die beiden bekannten
Variablen dienen jetzt in einer der drei Ursprungsgleichungen zur
Ermittlung der dritten Variablen.
Beispiele:
Das Darstellungs -Schema hat
sich bewährt!
1) x soll zuerst eliminiert werden .
| A) |
3x |
-2y |
+z |
= |
4 |
|*1 |
|
|
|
| B) |
-x |
+y |
+2z |
= |
-2 |
| *(3) |
A"+"3*B--->D |
|*2 |
|
| C) |
2x |
-y |
|
= |
2 |
|
|
|*1 |
2*B--"+"--C--->E |
Das ergibt das 2x2-System:
| D) |
y |
+7z |
= |
-2 |
|*(-1) |
-D--"+"--E--> F |
| E) |
y |
+4z |
= |
-2 |
|*1 |
|
Daraus folgt eine Gleichung mit einer Variablen:
| F) |
-3z |
= |
0 |
|
| : (-3) |
| |
z |
= |
0 |
|
|
Rückwirkend muss nun eingesetzt werden:
| E) |
y |
+0 |
= |
-2 |
|
|
| |
y |
|
= |
-2 |
|
|
| C) |
2x |
-(-2) |
= |
2 |
| -2 |
|
| |
2x |
|
= |
0 |
|
|
| |
x |
|
=0 |
|
|
Lösung: (0|-2|0) |
Unbedingt PROBE durch Einsetzen in alle
Ursprungsgleichungen machen!!!!
2)Diesmal soll y rausfallen. Das ist zwar die
umständlichste Möglichkeit, zeigt aber übungshalber den
möglichen Rechenaufwand
| A) |
3x |
+2y |
-4z |
= |
9 |
|*5 |
|
|*(-3) |
-3A --"+" --C--> E |
| B) |
x |
+5y |
+3z |
= |
16 |
|*(-2) |
5A--"+"--(-2B) -->D |
|
|
| C) |
2x |
+6y |
+z |
= |
19 |
|
|
|*1 |
|
| D) |
13x |
-26z |
= |
13 |
|*1 |
|
| E) |
-7x |
+13z |
= |
-8 |
|*2 |
D "+"--2E-->F |
| E) |
-7*3 |
+13z |
= |
-8 |
|
|
| |
|
13z |
= |
13 |
|
|
| |
|
z |
= |
1 |
|
|
| B) |
3 |
+5y |
+3*1 |
= |
16 |
|
| |
|
5y |
|
= |
10 |
|
| |
|
|
y |
= |
2 |
LÖSUNG: (3|2|1) Probe!! |
Anwendungen
Beispiel 1)
.......................................
| |
Typ 1 |
Typ 2 |
Typ 3 |
| Holzbretter |
1 |
2 |
4 |
| Stahlleisten |
2 |
1 |
1 |
| Schrauben |
1 |
2 |
1 |
|
Eine Firma stellt drei Typen von Regalen her. In der
Tabelle sind die benötigten Bestandteile
angegeben.(Angaben in "Sätzen". Am Lager
befinden sich 380 Sätze Holzbretter, 170 Sätze
Stahlleisten und 230 Sätze Schrauben. Wieviel Regale
können angefertigt werden?
|
a + 2b+ 4c = 380
2a + b+ c= 270
a+ 2b+ c= 230
Lösung:(20|80|50).....
|
Andere Anwendungen in (n
x n)-Systemen
Ein (4x4) -System wird
durch geeignete Wahl dreier
verschiedener Gleichungspaare wie oben auf ein (3x3)-System
reduziert und weiter berechnet. Dies lässt sich auf (n x
n)-Systeme ausweiten.
Beispiel 1) .................................................................
| ---B->20% A
--C->20%
---D->20%
|
| B <-A--30%
30%--C->
|
| 30%--B-> C
<-A--30%
|
| D <-A--40%
|
|
|
In vier Räumen A,B,C,D befinden sich 1000 Mücken.
Vom größten Raum A gibt es Öffnungen zu den kleineren
Räume B,C,D. Weiters gibt es eine Öffnung zwischen B
und C. Innerhalb einer Minute fliegen je 20 Prozent der
(sich in A befindenden) Mücken von A in die Räume
B,C,D. Vierzig Prozent derMücken in D fliegen nach A,
von B je 30 Prozent nach A und C, von C je 30 Prozent
nach A und B. In einer Minute können die Mücken in
höchstens einen anderen Raum fliegen. Nach einer Minute
sind 370 Mücken in A, 180 Mücken in B, 190 Mücken in C
und 260 Mücken in D. Wieviele Mücken waren am Anfang in
diesen Räumen? |
Lösung:(Zeichnung ist hilfreich!)
Man betrachtet, aus welchen Prozentanteilen (10% von A
=0,1a) sich die Räume nach einer Minute zusammensetzen
und erhält: A: 0,4a+0,3b+0,3c+0,4d=370
B: 0,2a+0,4b+0,3c =180
C: 0,2a+0,3b+0,4c =190
D: 0,2a +0,6d=260
Lsg: 400;300;200;100
|
Beispiel 2)
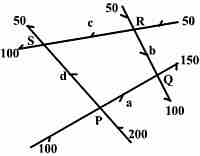
Die Abb. zeigt schematisch den Verkehrsfluß auf 4
Einbahnstraßen einer Stadt.Die Zahlen sind Schätzungen
für dieAnzahl der pro Stunde erwarteten Autos. Für die
weitere Planung solen Verkehrsdichten a,b,c,d bestimmt
werden. Insbesondere soll der kleinstmögliche
Verkehrsfluß zwischen den Kreuzungen P und Q ermittelt
werden.
|
Lösung: Wenn an einer Kreuzung kein
Stau entstehen soll, muß der ankommende Verkehr dem
abfließenden entsprechen: P: a+d = 300; Q: a+b = 250
R: b+c =100; S: c+d =150
-------------
--> a =300 -d; b = -50 +d; c= 150 -d
die Verkehrsdichte in den verbindungsstraßen kann
also durch die Anzahl d der fahrzeuge, die von P nach S
fahren, beeinflußt werden.Da negative Werte einen
verbotenen Gegenverkehr bedeuten, muß d zwischen 50 und
150 betragen.Die minimale Verkehrsdichte zwischen P und Q
hat demnach den Wert 150.
|
Die Quadratische
Ergänzung und die p,q- Formel
Um den Streit zu
beenden, womit man eine quadratische Gleichung löst, will ich
hier zeigen, dass die p,q- Formel nichts weiter ist als das
Ergebnis der Quadratische Ergänzung von 0 = x²+px+q
0 =
x²+px+q|-q
-q = x²+px
-q = (x+p/2)²
-(p/2)²
da (x+p/2)²=x²+px+(p/2)²
gilt, ist der letzte Summand "zuviel" und muß wieder
abgezogen werden.Das ist die "Quadratische Ergänzung":
-q+(p/2)² =(
x+p/2)²|Wurzel ziehen
(sqrt(...)
+/-
sqrt(-q+(p/2)²) = x +p/2
-p/2 +/-
sqrt(-q+(p/2)²) = x
x = -p/2
+/- sqrt((p/2)²-q)
