MATHE - Aufgabenberater
Funktionen sind Vorschriften, die jedem x NUR EIN y zuordnen. Gebilde wie "Kreise" oder "Schleifen" oder "Kringel" oder "Überlappungen" gehören zum Oberbegriff RELATION und müssen gesondert betrachtet werden.
Geometrische Abbildungen von Funktionsgraphen
und zugehörige Änderung der Funktionsterme
Zu den geometrischen Abbildungen gehören :
| Verschiebung nach oben | Vo | Stauchung längs x-Achse | Stax | Spiegelung an der x-Achse | Spx |
| Verschiebung nach unten | Vu | Stauchung längs y-Achse | Stay | Spiegelung an der y-Achse | Spy |
| Verschiebung nach links | Vli | Streckung längs x-Achse | Strx | Spiegelung an (0|0) | SpO |
| Verschiebung nach rechts | Vre | Streckung längs y-Achse | Stry |
| Geom. Abb. | Vo | Vu | Vre | Vli | Spy | Spx | SpO | Strx | Stax | Stry | Stay |
| neuer Term | f(x)+a | f(x-b) | f(-x) | -f(x) | -f(-x) | f(x/c) | d*f(x) | ||||
| a>0 | a<0 | b>0 | b<0 | c>1 | 0<c<1 | d>1 | 0<d<1 | ||||
| x-->f(x) = x | x+a | (x-b) | -x | -x | -(-x) = x | x/c | d*x | ||||
| x-->f(x) = |x| | |x|+a | |x-b| | |-x| | -|x| | -|-x| | |x/c| | d*|x| | ||||
| x-->f(x) = 1/x | (1/x) +a | 1/(x-b) | 1/(-x) | -(1/x) | -(-(1/x)) | 1/(x/c) | d*(1/x) | ||||
| x-->f(x) = sin x | sinx+a | sin(x-b) | sin(-x) | -sinx | -sin(-x) | sin(x/c) | d*sinx | ||||
| x-->f(x)= mx+n | mx+n+a | m(x-b)+n | m(-x)+n | -(mx+n) | -(m(-x)+n) | m(x/c)+n | d*(mx+n) | ||||
| x-->f(x) = e^x | e^x+a | e^(x-b) | e^(-x) | -e^x | -e^(-x) | e^(x/c) | d*e^x | ||||
| x-->f(x)=x² | x²+a | (x-b)² | (-x)² | -x² | -(-x)² | (x/c)² | d*x² |
Das lässt sich mit einem geeigneten Darstellungstool eines Matheprogramms (offline z.B. WINFUNKTION) leicht nachprüfen.
Es sind daraus mit etwas Routine Kombinationen zu verknüpfen, z.B. erst die Verschiebung nach oben und dann die Spiegelung an der y- Achse und zum Schluss eine Streckung Richtung x-Achse:
Beispiele:
| 1) f(x) --> g(x) = f(x)+a --> h(x) = -g(x) -->k(x) =h(x/c) - speziell: f(x) = cos (x) -->g(x) = cos(x)+a --> h(x)= -(cos(x)+a) -->k(x) = -(cos (x/c)+a) = -cos(x/c)-a |
2) f(x) --> g(x) = f(x-b)--> h(x) = d*g(x) -->k(x) = h(x) +a speziell: f(x) = x²--> g(x) =(x-b)² --> h(x) = d*(x-b)² --> k(x)= d*(x-b)²+a (Scheitelpunktform der Parabel) |
Bestimmung der Umkehrfunktion f^(-1)
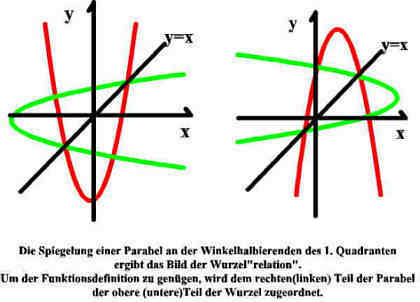
Rein zeichnerisch bedeutet das, die Funktion an der Winkelhalbierenden zu f(x) = x zu spiegeln. Algebraisch wird dazu "x" und "y" in der Funktionsgleichung vertauscht und nach dem neuen "y" aufgelöst. dabei entsteht nicht immer automatisch eine neue Funktion - es können auch Relationen auftreten.In der Sek I behandelt man in eigentlich kaum mehr als vier Typen, die immer nach dem jeweils gleichen Schema bestimmt werden können:
| f(x) = y =ax +b x <-vertauscht -> y: x =ay+b ----> x-b= ay 1/a*(x-b) = y = f^(-1)[(x)] |
f(x)= y= (ax-b)/cx-d) x <-vertauscht -> y: x =(ay-b)/cy-d) ---> x(cy-d)=ay-b -->xcy-dx=ay-b --->xcy-ay=dx-b --->y(cx-a)=dx-b (dx-b)/(cx-a) = y = f^(-1)[(x)] |
f(x)= y = a*sqrt (bx-c)+d (sqrt (..)="Wurzel aus ....") x <-vertauscht -> y: x=a*sqrt(by-c)+d x-d =a*sqrt(by-c) |( )²--> (x-d)²=a²(by-c) --> [(x-d)/a]²=by-c (1/b)*([(x-d)/a]²+c) = y = f^(-1)[(x)] |
f(x) =y= a(bx-c)²+d x <-vertauscht -> y: x =a(by-c)²+d x-d =a(by-c)²--->(x-d)/a=(by-c)² | sqrt (+/-)sqrt((x-d)/a)=by-c (1/b)*(c+sqrt((x-d)/a) =y´ (1/b)*(c-sqrt((x-d)/a) =y´´ (2 Lösungen) |
Bei einer Parabel f(x) = a(bx-c)²+d gibt es Probleme, weil bei der Spiegelung an y=x eine Relation herauskommt. Allerdings funktionieren die Methoden wieder mit Fallunterscheidung: Dann gehört jede der beiden Lösungen zu einer eigenen Hälfte der Parabel.

Bestimmung der Symmetrie
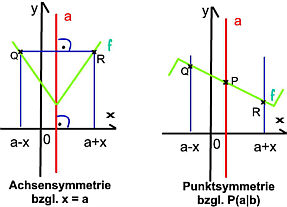
Bei Achsensymmetrie an x = a gilt:
f(a+x) = f (a-x)
Alle Punkte Q,R , die gleich weit von der senkrechten Achse entfernt sind, haben den selben Funktionswert.
Bei Punktsymmetrie an P(a|b)) gilt:
f(a-x)+f(a+x) = 2b.
Wenn man die Gleichung durch 2 teilt, erkennt man: b ist der Mittelwert der Funktionswerte von Q und R.