 |
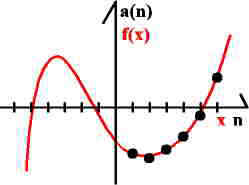
f(x) = sx^5
+tx^4+ux^3+vx^2+wx+z a(n) = sx^5+tx^4+ux^3+vx^2+wx+z n ist immer positiv, bei f gibtes auch die roten Zwischenwerte |
MATHE - Aufgabenberater
Folgen und Reihen
Eine Folge ordnet jedem n> 0 einen Wert a(n) zu.
| a(n)/n | 1 | 2 | 3 | 4 | ... | 10 | ... | 121 | ... | 1500 | ... |
| n² | 1 | 4 | 9 | 16 | 100 | 14641 | 2250000 | ||||
| n³ | 1 | 8 | 27 | 64 | 1000 | ... | .... | ||||
| 4n | 4 | 8 | 12 | 16 | 4000 | 484 | 6000 | ||||
| (-1)^n | -1 | 1 | -1 | 1 | 1 | -1 | 1 | ||||
| n+7 | 8 | 9 | 10 | 11 | 17 | 128 | 1507 | ||||
| 2n/(n-3) | -1 | -4 | -- | 8 | 20/7 | 242/11 | 3000/1497 | ||||
| (-1)^n(4n+1) | -5 | 9 | -13 | 17 | 41 | -485 | 6001 | ||||
| 5/n | 5 | 5/2 | 5/3 | 5/4 | 5/10 | 5/121 | 5/1500 | ||||
| (n+2)/(n-1) | -- | 4 | 5/2 | 2 | 12/9 | 123/120 | 1502/1499 |
Der Unterschied zwischen Folge und Funktion
 |
f(x) = sx^5
+tx^4+ux^3+vx^2+wx+z a(n) = sx^5+tx^4+ux^3+vx^2+wx+z n ist immer positiv, bei f gibtes auch die roten Zwischenwerte |
Wie erkennt man eine Folge?
Wenn du so etwas
| 1;8,27,64,.. | 3;6;12;24;... | -(1/2);1;-(5/4);7/5;... | 2;5;8;11;.. | 2;4/3;6/5;8/7;... |
als Folge erkennen sollst, musst du zuerst jeden Wert dem entsprechenden "n" zuordnen und dabei bei n=1 beginnen:
|
|
|
|
|
Wenn sich "+" und "-" abwechseln, ist immer ein (-1)^n im a(n)-Term vorhanden.
Mache vorher aus gemischten Zahlen IMMER geeignete echte Brüche!
Jetzt ist Erinnerungsvermögen und mathematisches Gespür gefragt: Wie hängt der obere Term mit der Zahl darunter zusammen?
Aber meist reicht auch ein systematischer Check nach den wichtigsten Möglichkeiten, d.h. den ersten 5 Beispielen aus der allerersten Tabelle auf dieser Seite oder den
Potenzen (1^n;2^n;3^n;..), Summen,Differenzen (n+x; n-x), Produkten (xn; (a/b)n..), gerade Zahlen(2n), ungerade Zahlen(2n-1) und Kombinationen daraus.
| Bei der ersten Aufgabe findest du somit sofort a(n) = n^3. | Beim 2. Beispiel ist nach intensiver
Betrachtung eine Veränderung angebracht:.
Dabei fällt dann irgendwann auf, dass die 3 mit den "verrutschten" Zweierpotenzen multipliziert wird. (2^0 =1!)
Das führt dann zu a(n) =3*2^(n-1) |
||||||||||||||||||||||||||||||||||||||||||
Die dritte Aufgabe bedarf einer kleinen (geeigneten, deshalb die Drittel!)Verwandlung in durchweg echte Brüche:
|
Du erkennst sofort, dass alles mit (-1)^n
multipliziert werden muss, weil die Vorzeichen
regelmässig wechseln. Ausserdem muss im Nenner einfach
"n" stehen. im den Zählern stehen die
ungeraden Zahlen. Also gilt: a(n) =[(-1)^n]*[(2n-1)/n] |
||||||||||||||||||||||||||||||||||||||||||
| Im vierten Beispiel findest du, dass der
Unterschied immer 3 beträgt. Dass lässt auf 3*n schließen.Da im Ergebnis aber immer einer weniger rauskommt, gilt: a(n)=3*n-1 Überprüfe die methodik an a(n) = 4n+5 und a(n)= 2n-4! |
Das 5. Beispiel wird wieder zuerst
eingepasst:
Im Zähler sind die geraden, imNenner die ungeraden Zahlen --> a(n)= (2n)/(2n-1). |
Vollständige Induktion
Allgemein:
Ich nehme an, dass A(n) gilt. A(n) ist die Aussage schlechthin.
Dann bilde ich A(n+1) , indem ich überall das "n" durch ein "(n+1)" ersetze. Dann versuche ich dies solange umzuformen, bis A(n) wieder auftaucht und benutze, dass für diesen Teil die Voraussetzung A(n) gilt.
Mal ein allgemeiner Tip anhand
des Beweises von
1²-2²+3²-4²+....+(-1)^(n-1)*n² =(-1)^(n-1)*n/2*(n+1)
für den finalen Schritt von
A(n) zu A(n+1):
Ich addiere auf beiden Seiten das (n+1)te Glied, lasse genügend
Platz und schreibe hinter das Gleichheitszeichen in der letzten
Zeile das komplette (n+1) - Ergebnis.
1²-2²+3²-4²+...+(-1)^(n-1)*n² +(-1)^n*(n+1)² |
= (-1)^(n-1)*n/2*(n+1)+(-1)^n*(n+1)² |
| =... | |
| =... | |
| =... | |
| =... | |
=(-1)^(n)*((n+1)/2)*(n+2) |
Dann versuche ich mich mit Umformungen von oben und unten
gleichzeitig an eine gemeinsame Zeile irgendwo in der Mitte
heranzuarbeiten.
Ein anderes Beispiel:
3 teilt 2 + 13^n
Für n= 1,2.. gilt die Behauptung: A(1) -->
3 teilt 15; A(2) -->3 teilt 171
Angenommen, es giltA(n) = 2+13^n. --> Bilde A(n+1) =
2+13^(n+1)
Jetzt muss man das irgendwie in Abhängigkeit von A(n) bringen:
2+13^n*13^1 = 2+(-2+2+13^n)*13 = 2-26 +(2+13^n)*13 = -24
+(2+13^n)*13
-24 teilt 3, die Klammer teilt 3 nach Annahme und somit teilt das
Produkt auch 3. q.e.d.